I have recently played around with Stan, which is an excellent software to fit Bayesian models. It is similar to JAGS, which I have used before to fit some regression models for predicting football results. Stan differs from JAGS in a number of ways. Although there is some resemblance between the two, the model specification languages are not compatible with each other. Stan, for instance, uses static typing. On the algorithmic side, JAGS uses the Gibbs sampling technique to sample from the posterior; Stan does not do Gibbs sampling, but has two other sampling algorithms. In Stan you can also get point estimates by using built-in optimization routines that search for the maximum of the posterior distribution.
In this post I will implement the popular Bradley-Terry machine learning model in Stan and test it on some sports data (handball, to be specific).
The Bradley-Terry model is used for making predictions based on paired comparisons. A paired comparison in this context means that two things are compared, and one of them is deemed preferable or better than the other. This can for example occur when studying consumer preferences or ranking sport teams.
The Bradley-Terry model is really simple. Suppose two teams are playing against each other, then the probability that team i beats team j is
\( p(i > j) = \frac{r_i}{r_i + r_j} \)
where \(r_i\) and \(r_j\) are the ratings for the two teams, and should be positive numbers. It is these ratings we want to estimate.
A problem with the model above is that the ratings are not uniquely determined. To overcome this problem the parameters need to be constrained. The most common constraint is to add a sum-to-one constraint
\( \sum_k r_k = 1 \)
I will explore a different constraint below.
Sine we are in a Bayesian setting we need to set a prior distribution for the rating parameters. Given the constraints that the parameters should be positive and sum-to-one the Dirichlet distribution is a natural choice of prior distribution.
\( r_1, r_2, …, r_p \sim Dir(\alpha_1, \alpha_2, …, \alpha_p) \)
where the hyperparameters \(\alpha\) are positive real numbers. I will explore different choices of these below.
Here is the Stan code for the Bradley-Terry model:
data {
int<lower=0> N; // N games
int<lower=0> P; // P teams
// Each team is referred to by an integer that acts as an index for the ratings vector.
int team1[N]; // Indicator arrays for team 1
int team2[N]; // Indicator arrays for team 1
int results[N]; // Results. 1 if team 1 won, 0 if team 2 won.
vector[P] alpha; // Parameters for Dirichlet prior.
}
parameters {
// Vector of ratings for each team.
// The simplex constrains the ratings to sum to 1
simplex[P] ratings;
}
model {
real p1_win[N]; // Win probabilities for player 1
ratings ~ dirichlet(alpha); // Dirichlet prior.
for (i in 1:N){
p1_win[i] = ratings[team1[i]] / (ratings[team1[i]] + ratings[team2[i]]);
results[i] ~ bernoulli(p1_win[i]);
}
}
The way I implemented the model you need to supply the hyperparameters for the Dirichlet prior via R (or whatever interface you use to run Stan). The match outcomes should be coded as 1 if team 1 won, 0 if team 2 won. The two variables team1 and team2 are vectors of integers that are used to reference the corresponding parameters in the ratings parameter vector.
Before we fit the model to some data we need to consider what values we should give to the hyperparameters. Each of the parameters of the Dirichlet distribution corresponds to the rating of a specific team. Both the absolute magnitude and the relative magnitudes are important to consider. A simple case is when all hyperparameters have the same value. Setting all hyperparameters to be equal to each other, with a value greater or equal to 1, implies a prior belief that all the ratings are the same. If they are between 0 and 1, the prior belief is that the ratings are really really different. The magnitude also plays a role here. The greater the magnitudes are, the stronger the prior belief that the ratings are the same.
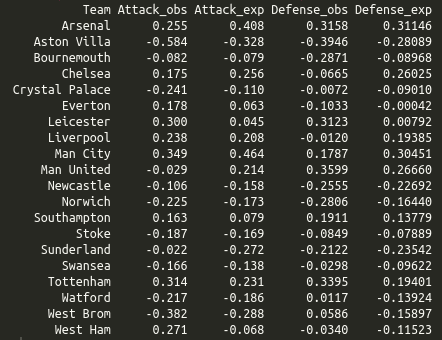
Let’s fit some data to the model. Below are the results from fitting the results from 104 games from the 2016-17 season of the Norwegian women’s handball league, with 11 participating teams. I had to exclude six games that ended in a tie, since that kind of result is not supported by the Bradley-Terry model. Extension exists that handle this, but that will be for another time.
Below are the results of fitting the model with different sets of priors, together with the league points for comparison. For this purpose I didn’t do any MCMC sampling, I only found the MAP estimates using the optimization procedures in Stan.

For all the priors the resulting ratings give the same ranking. This ranking also corresponds well with the ranking given by the league points, except for Gjerpen and Stabæk which have switched place. We also clearly see the effect of the magnitude of the hyperparameters. When all the \(\alpha\)‘s are 1 the ratings varies from almost 0 to about 0.6. When they are all set to 100 the ratings are almost all the same. If these ratings were used to predict the result of future matches the magnitudes of the hyperparameters could be tuned using cross validation to find the value that give best predictions.
What if we used a different hyperparameter for each team? Below are the results when I set all \(\alpha\)‘s to 10, except for the one corresponding to the rating for Glassverket, which I set to 25. We clearly see the impact. Glassverket is now considered to be the best team. This is nice since it demonstrates how actual prior information, if available, can be used to estimate the ratings.

I also want to mention another way to fit the Bradley-Terry model, but without the sum-to-one constraint. The way to do this is by using a technique that the Stan manual calls soft centering. Instead of having a Dirichlet prior which enforces the constraint, we use a normal distribution prior. This prior will not give strict bounds on the parameter values, but will essentially provide a range of probable values they can take. For the model I chose a prior with mean 20 and standard deviation 6.
\( r_1, r_2, …, r_p \sim N(\mu = 20, \sigma = 6) \)
The mean hyperprior here is arbitrary, but the standard deviation required some more considerations. I reasoned that the best team would probably be in the top 99 percentile of the distribution, approximately three standard deviations above the mean. In this case this would imply a rating of 20 + 3*6 = 38. Similarly, the worst team would probably be rated three standard deviations below the mean, giving a rating of 2. This implies that the best team has a 95% chance of winning against the worst team.
Here is the Stan code:
data {
int<lower=0> N;
int<lower=0> P;
int team1[N];
int team2[N];
int results[N];
real<lower=0> prior_mean; // sets the (arbitrary) location of the ratings.
real<lower=0> prior_sd; // sets the (arbitrary) scale of the ratings.
}
parameters {
real<lower=0> ratings[P];
}
model {
real p1_win[N];
// soft centering (see stan manual 8.7)
ratings ~ normal(prior_mean, prior_sd);
for (i in 1:N){
p1_win[i] = ratings[team1[i]] / (ratings[team1[i]] + ratings[team2[i]]);
results[i] ~ bernoulli(p1_win[i]);
}
}
And here are the ratings for the handball teams. The ratings are now on a different scale than before and largely matches the prior distribution. The ranking given by this model agrees with the model with the Dirichlet prior, with Gjerpen and Stabek switched relative to the league ranking.