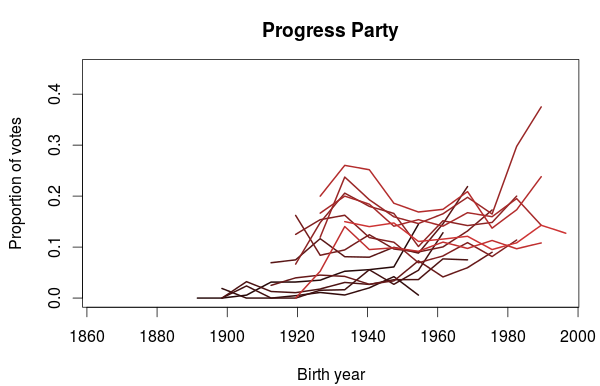
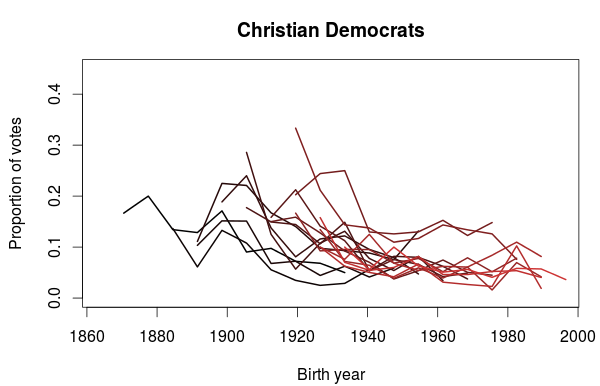
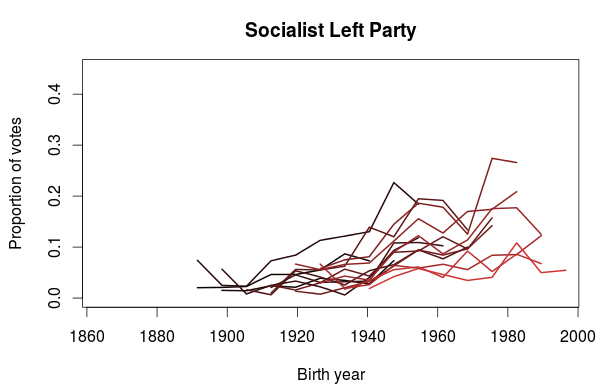
In the last post I used data from the Norwegian election survey to look at how party preferences changed between generations. One thing I didn’t look at was if there was any differences in participation between the generations. While the Norwegian elections generally has a high turnout, the general trend has been a decline. Some numbers on voter turnout are available from Statistics Norway, and a plot of turnout for the national elections for parliament and the local elections show that this is especially true for the local elections. For the parliament elections there seems to be a sudden drop in turnout at the 1993 election. Before that the general turnout was somewhere between 80% and 85%. From 1993 and onwards it has been somewhere between 75% and 80%.
This time I decided to only look at the surveys done in connection with the parliamentary elections. This was to avoid much clutter with the differences between the local and national elections. After I gathered the data from the elections surveys using the web analysis tool at the web page for Norwegian Center For Research Data (see the link above), I plotted the voter turnout for each election for each birth cohort (in 7-year groups). In the plot is each election represented by a line. The same thing I did in the previous post, in other words.
We clearly see a trend in which younger generations, those born after about 1955, are less likely to vote. But there is also a clear indication that the young voters, when they get older, are more likely to vote. This trend can for example be seen for the 1970-generation. The earliest generations where this group could vote are those lines where the line ends in about 1970. In the earliest elections where this group could vote, more than 25% did not vote, but in the more recent elections only 10% of this generation did not vote.
Also notice how in each election, the oldest group also seem to have a tendency to not vote. This could perhaps be explained by the older population generally has poorer health and will therefore not prioritize to get out to vote. But I also suspect this is partially explained by random variation, as the oldest birth groups have relatively few respondents in the surveys.
We can plot the turnout by age instead of birth year to get a better view of the differences between age groups. Here I used 5-year groups instead of 7. In this plot the lines do seem to align a bit better.
Still another figure we could do is to plot the turnout for different age groups, and then see how this has changed from election to election. Here I have plotted only two age groups, those 25 or younger, and those older than 25. Also shown is the national turnout, which is not from the election survey, but are the official turnout numbers. This is the same as in the first plot above.
We see again that the young voters have lower turnout than the older ones, which by now should be no surprise. In addition, the difference between the young and the old seem follow each other between the elections to a large degree, going up and down in a similar pattern, but it also become noticeably wider from the 1993 election. From just looking at this plot, it could seem as if the lower turnout among the young could explain a lot of the decrease that happened in the 1993 election, but keep in mind that the younger group is a relatively small group. Not pictured in the plot is the uncertainty of the estimates, which gives the unreasonable results in the 1965 and 1985 elections, where both the young and old have higher turnout (as measured by the survey) than the official numbers.
So from looking at these plots, it seems like when people where born, what age you are and which election it is influence whether you vote or not. But the effect of these three aspects is hard, if not impossible, to untangle. The reason for this is simple: How old you are is fully determined by when you are and when you were born. You can of course turn it around and say the same for the two other aspects: If you know two of them, you also know the third. From a modeling point of view this dependency makes it hard to put these three variables in a regression model, but there are some literature out there on how this kind of Age-Period-Cohort analysis (as it is called) could be done.
But does this mean we can’t really learn anything from it? I think we can. The kind of analysis like the one I have done here is of course rather informal and descriptive, no p-values or effect sizes or stuff like that, but I think it is clear that age plays an important role. The third plot, with age on the horizontal axis, looks much nicer than the second plot, with birth year on the horizontal. The lines align rather nicely. We can also see this in the cohort plot, where the 1970-generation had a low turnout in the first elections they could participate in, but in the more recent elections they participate as much as those born before that.
Whether the changes in participation among the young over time is a period effect or a cohort effect is more difficult to say. It seems to covary with the general trend, but it also has it’s own component. This does not seem to play a large role, except perhaps a change at the 1985 election (or among those born in the 1960’s, depending on your view).