I had a discussion with some friends the other day about separate sports competitions for men and women. In some sports, like curling, it seems rather unnecessary to have separate competitions. At least assuming the reason for gendered competitions is that being a male or a female may give the competitor an obvious advantage. One sport where we didn’t think it was obvious was ski jumping, so I decided to look at some numbers.
This year’s Olympics was the first time women competed in ski jumping so decided to do a quick comparison of the results from the final round in the men’s and women’s final.
This is what I came up with:
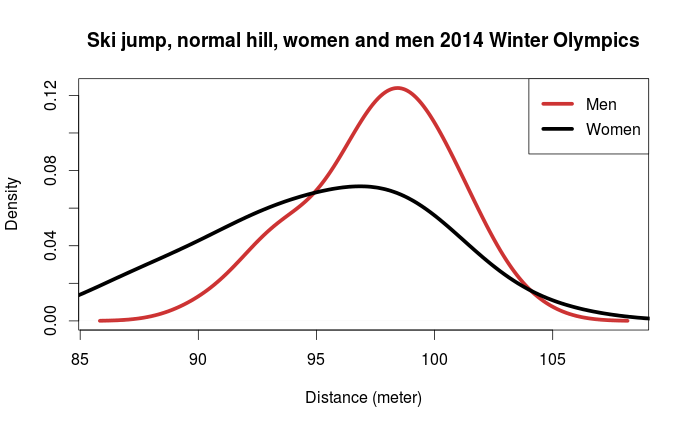
What we see are the estimated distributions for the jump distances for men and women. The mode for the women seems to be a little lower than the mode for the men. We also see that there is much more variability among the women jumpers than among the men and that the women’s distribution have a longer right tail. Still, it looks like the best female jumpers are on par with the best male jumpers and vice verca.
The numbers I used here are not adjusted for wind conditions and other relevant factors, so I will not draw any firm conclusions. I hope to have time to look more into this later, using data from more competitions, adjusting for wind etc.