In the last post I discussed how to tune the Elo ratings to make the ratings have the best predictive power by finding the optimal update factor (the K-factor) and adjustment for home field advantage. One thing I only mentioned, but did not go into detail about, was that the teams initial ratings will influence this tuning. In this post I will show how we can find good initial ratings that also will mitigate some other problems associated with Elo ratings.
As far as I can tell, setting the initial ratings does not seem to be much discussed. The Elo system updates the ratings by looking at the difference between the actual results and the results predicted by the rating difference between the two opposing teams. To get this to work in the earliest games in the data, you need to supply some initial ratings.
It is possible to set the initial ratings by hand, using your knowledge about the strengths of the different players and teams. This strategy is however difficult to use in practice, since you may not have that knowledge, which in turn would give incorrect ratings. This task would also become more difficult the more teams and players are in your data. An automatic way to get the initial ratings is of course preferable.
The only automatic way to set the initial ratings I have seen is to set all ratings to be equal. This is what they do at FiveThirtyEight. This simple strategy is obviously not optimal. It is a bit far fetched to assume that all teams are equally good at the beginning of your data, even if you could argue that you don’t really know any better. If you have a lot of data going back a long time, then only the earliest period of your ratings will be unrealistic. After a while the ratings will become more realistic and better reflect the true strengths of the teams.
The unrealistic ratings for the earliest data may also cause a problem if you use this to find the optimal K-factor. In Elo ratings the K-factor is a parameter that determines how much new games will influence the ratings. A larger K-factor makes the ratings change a lot after a new game, while a low K-factor will make the ratings change only a little after each new game. If you are trying to make a rating system with good prediction ability and use the earliest games with the unrealistic ratings to tune the K-factor, then it will probably be overestimated. This is because a large K-factor will make the ratings change a lot at the beginning, making the ratings better quicker. A large K-factor will be good in the earliest part of your data, but after a while it may be unrealistically big.
One more challenge with Elo ratings is if you include multiple leagues or competitions in your rating system. Since the Elo ratings are based on the exchange of points, groups of teams that play each other often, such as the teams in the same league, will have ratings that are reasonable calibrated only between each other. This is not the case when you have teams from different leagues play each other. The rating difference between two teams from two leagues will not be as well-calibrated as those within a league.
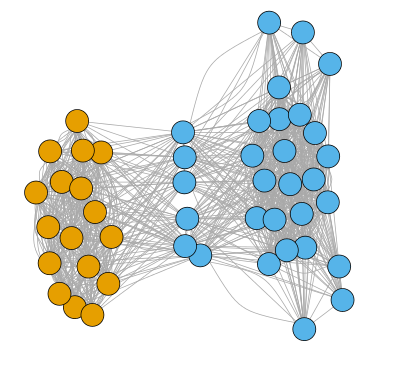
A nice visualization of this is to plot which teams in your data have played each other. In the plot below each team is represented by a circle, and each line between the circles indicates that the two teams have against played each other. The data is from Premier League and the Championship from the year 2010; two half-seasons for each division. I haven’t added team names to the graph, but the orange circles are the teams that played in the Premier League in both seasons, while the blue circles are teams that played in the Championship or got promoted or relegated.
We clearly see that the two division cluster together with a lot of comparisons available between the teams. Six teams, those that got promoted and relegated between the two divisions, are clearly shown to fall in between the two large clusters. All comparisons to be made between teams in the two divisions has to rely on the information that is available via these six teams. Including all these teams in a Elo rating, starting with all ratings equal, will surely be completely wrong and will take some time to be realistic. All point exchange between the divisions will have to happen via the promoted and relegated teams.
I have previously investigated this in the context of regression models, where I demonstrated how including data from the Championship improves the prediction of Premier League matches. Se this and this.
So how can we find the initial ratings that will give realistic ratings that also calibrate the ratings between two or more leagues? By using a small amount of data, say one year worth of data, less that you would use to tune the K-factor and home field advantage, you can use an optimization algorithm to find the ratings that best fits the observed outcomes. In doing this you have to use the formula that converts the ratings to expected outcomes, but you do not use the update formula, so this approach can be seen as a static version of the Elo ratings.
Doing the direct optimization is however not completely straightforward. Elo ratings is a zero-sum system. No points are added or removed from the system, only exchanged. This constraint is similar to the sum-to-zero constraint that is sometimes used in regression modeling and Analysis-of-Variance. To overcome this, we can simply set the rating of one of the teams to the negative sum of the ratings of all the other teams.
A further refinement is to include home field advantage into the optimization. In cases where the teams have unequal number of home games, or some games where no teams play at home, this will create more accurate ratings. If not the ratings for those teams with an excess of home games will become unrealistically large.
Doing this procedure, using data from the Premier League and the Championship from 2010 which I used to make the graph above, I get the following ratings (with the average rating being 1500):
The procedure also estimated the home field advantage to be 84.3 points.
The data I used for the initial ratings is the first year of the data I used to tune the K-factor in the previous post. How does using these initial ratings influence the this tuning, compared with using the same initial rating for all teams? As expected, the optimal K-factor is smaller. The plot below shows that K=14 is the optimal K, compared with K=18.5 that I found last time. It is also interesting to see that the ratings with initialization are more accurate for the whole range of K’s I tested, than those without.